Container with most water
You are given an integer array height of length n. There are n vertical lines drawn such that the
two endpoints of the ith line are (i, 0) and (i, height[i]).
Find two lines that together with the x-axis form a container, such that the container contains the most water.
Return the maximum amount of water a container can store.
Notice that you may not slant the container.
Example
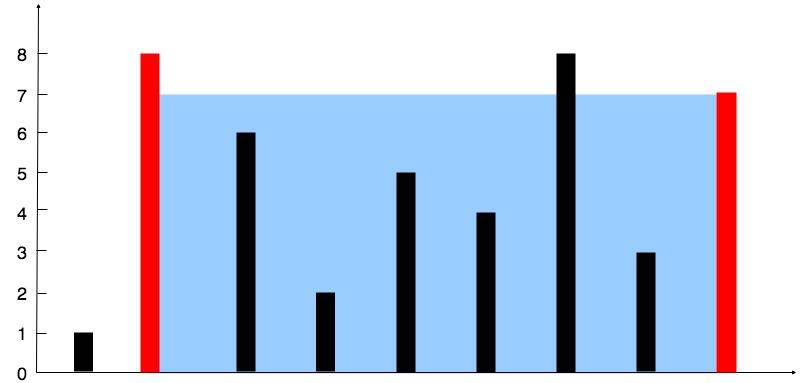
- Input:
height = [1,8,6,2,5,4,8,3,7] - Output: 49
- Explanation: The above vertical lines are represented by array [1,8,6,2,5,4,8,3,7]. In this case, the max area of water (blue section) the container can contain is 49.
Solution (Java)
I like this problem because it makes use of the two-pointer techniques in a real scenario.
Especially because it’s an optimization problem but does not rely solely on math.
Note that similar to the two-sum (sorted) problem, we can use two pointers i,j, one at the beginning one at the end.
This gives us a water container which has the largest possible width, meaning moving any pointer (i to the right or j to the left) would result to
a smaller width. Since we need to optimize for area, we have to find a higher line which makes the
container narrower but would still result to a larger area. Now the question is, do we move i or j?
Clearly, this depends on the height of the two and if height[i] is shorter than height[j] that means, we need to optimize
the line in i and we move to the right. The same applies vice-versa. With this technique, we searched the whole array in O(n).
class Solution {
public int maxArea(int[] height) {
int maxArea = 0;
int n = height.length;
int i = 0; int j = n-1;
while(i != j){
if(Math.min(height[i], height[j])*(j-i) > maxArea){
maxArea = Math.min(height[i], height[j])*(j-i);
}
if(height[i] < height[j]){
// move i to the right
i++;
}else{
j--;
}
}
return maxArea;
}
}